【貨幣循環】に基づいた政府支出の成長率とGDPの成長率の正比例関係の説明 まとめ

本記事では、政府支出の成長率（dG/G）とGDPの成長率（dY/Y）の正比例関係について、貨幣循環の視点での定量的な説明の締めとなります。本記事の後半では、日本とアメリカのGとIの（ほぼ）正比例関係の図を示し、さらにdG/Gに対してのdY/YとdV/V（貨幣循環速度の成長率）の分布を示します。これらの分布によって示される定量的な関係を使うと、「M=G+I、V=1/(1-β)」の関係式から「dY/Y=dG/G」を導くことができます。

以下、本記事の内容です。

1. dG/GとdY/Yの正比例関係についての、これまでの記事まとめ。
2. 日本とアメリカのGとIの年変化。
3. OECDのデータによる、dG/G、dY/Y、dV/Vの関係。
4. まとめ。

1. dG/GとdY/Yの正比例関係についての、これまでの記事まとめ。

ここからスタート、「【貨幣循環】貨幣循環導入の3点セット」

• 貨幣循環てなんだろうね？なんでGDPの計測はあの式なの？貨幣循環速度の見積もり方法、精度悪すぎて草。
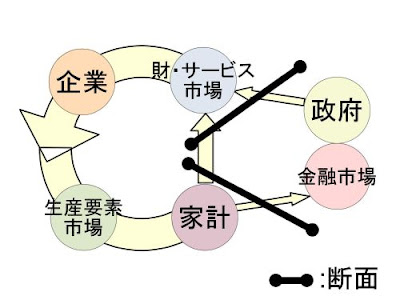
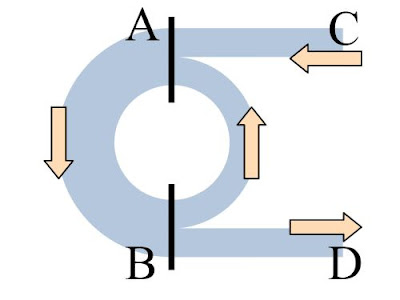
• 循環フロー図、GDP測定式、Y=MV=PQを悪魔合体。
• これらの一貫した描像から次の関係が得られる。M=G+I、V=1/(1-β)。貨幣の流れを考えたらM=G+I。CとT+Sの割合の指標であるβなら、循環速度のキーパラメータとして納得。

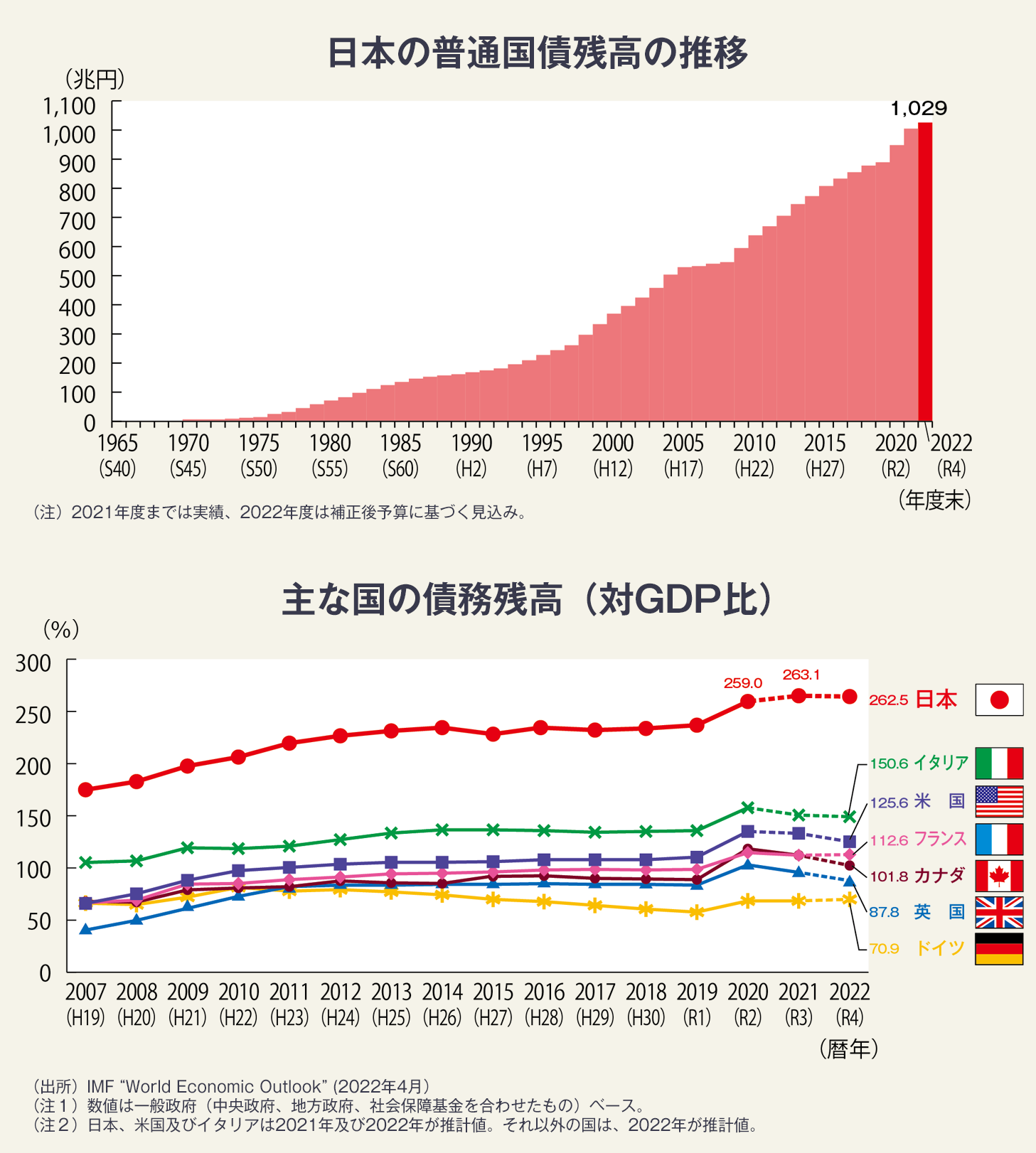
なんかdG/GとdY/Yの正比例関係というのがあるらしい。「【貨幣循環】歳出伸び率とGDP成長率の関係（MVとMの各変化率の関係）」

• あれ、M=G+I、V=1/(1-β)をいじったら、dG/GとdY/Yの正比例関係を説明できそうですね。
• 必要な条件は、G~I、dV/V=0。どこにデータがあるかな？

OECDからデータとってきたわ。「【貨幣循環】貨幣循環速度Vの成長率 （33カ国、最近20年間のデータ）」

• dV/Vの平均値は0付近に分布。
• βの範囲は0から1。それに対して政府支出は桁で増加し続けるため、dG/Gに比べてdV/Vが小さいのは納得のいく話。
• OECDにはなんで投資（I）のデータがないんや…。

2. 日本とアメリカのGとIの年変化。

以下、日本とアメリカのGとIの年変化です。

日本のGとIの年変化。横軸がG、縦軸がI。縦軸横軸ともにログスケールです。シンボルの違いは取得データの違いです。（データの説明は今後追記します。といってももちろん政府発行のデータです。）

アメリカのGとIの年変化。横軸がG、縦軸がI。縦軸横軸ともにログスケールです。

日本の場合はGとIの正比例関係！、とはいいがたい時代もありますが、係数の変化はあれどGとIが比例していることに変わりはありません。従って、例えばG=aIとおくことができます。従って、dM/M = d(G+I)/(G+I) = dG(1+a)/[G(1+a)] = dG/Gが得られます。

3. OECDのデータによる、dG/G、dY/Y、dV/Vの関係。

以前のdV/Vの図と同じデータセットで、dG/Gに対してのdY/Y（青丸印）とdV/V（緑丸印）の分布です。実線は、傾き1で原点を通る直線です。

この図からは、それなりの分散はあるものの、dV/Vの平均的な変化量は0近傍であり、それに比べてdG/GとdY/Yが正比例関係をみせていることが分かります。（緑丸の一点がすごい位置にありますが、、、）

従って、二番目の記事での数式の展開で示したように、G=aIとdV/V=0から、dY/Y=dG/Gの関係を示すことができました。

4. まとめ

みなさん、超弦理論（超ひも理論）はご存じですか？ちょっと古いかもしれませんが。私は全く理解できません。ただ科学者として言えることは、超ひも理論を含めた科学の多くの理論は、より多くの自然現象を説明しようという試みだということです。そういう試みが積み重なって現在の科学は形成されています。

貨幣循環に基づいた私の仮説は、超ひも理論よりずっと単純です。しかしながら、私の仮説はGDPの測定式と貨幣循環を矛盾なく説明し、精度の良い貨幣循環速度（M=G+I, V=1/(1-β)）を導きます。そして今回のdG/GとdY/Yの正比例関係も説明できました。この仮説は、貨幣循環に基づいてマクロ経済の大事な要素を説明できています。

私はこの仮説が、需要と供給の観点に基づいた現在のマクロ経済学よりも、マクロ経済の一部分を、おそらくは核心的な一部分をよく説明できていると思います。さきほどの超ひも理論の節で言及しましたが、より多くの自然現象を説明できるのが良い仮説です。私の仮説は説明できることはまだ少ないですが、マクロな経済現象を説明するための方向性はそれほど悪くないと考えます。

経済学物理学クイズ、水路に流入した水は何回転したか？

以下、クイズの概要を述べ、次に細かい設定を述べます。

水路についての数量A、B、Cが与えられます。このABCを使って、水源（蛇口）から水路に流入した水が水路を何回循環し、水路から流出するのか、概算できる二つの式を与えます。どちらの概算が適切か、選択してください。

広大な水路（ブラックボックス）＋水源＋貯水池＋水源と貯水池の間の水路。

• 一定期間、水源（蛇口）から流れ出た水量はA。（ある断面で測定。A>0）
• 一定期間、水源と貯水池の間の水路を流れる水量はB。（ある断面で測定。B>0）
• これまでの全期間において、水路から貯水池へと流れた水量はC。
• 簡単のために定常状態。水量A、Bは時間的に変化しない。
• 広大な水路（ブラックボックス）は閉じている。

選択肢である概算式。

概算式その一、(A+B)/A。    

概算式その二、(A+B)/C。

「循環の回数を求めるのに、概算式その二なんかありえんやろ」と思った科学者技術者あるいはその卵かもしれないアナタm9(・ω・)！第３節「本問題の意味」へどうぞ。

内容

1. 問題設定詳細
2. 選択肢（概算式）
3. 本問題の意味

問題設定詳細

循環回数の概算をしたいので物理学っぽい感じで記述しています。理想的な状況を考えています。好意的に解釈してください。

• その水路は皆が利用しています。しかし水路はとても広大なため、一人がその全貌を把握することは困難です。そのためにブラックボックスとなっています。
• 水源と貯水池の間の区間は、水路が収束しています。この区間は、水路全体の長さに対して十分短い区間です。この区間の上流では一定量の水が貯水池に流れ出ています。その下流では一定量の水が水源から流れ込んでいます。簡単のために、この両者の水量は同量、時間的に変化しない、と仮定します。
• この水路では、一か月に一度、水が循環しています。回転速度、循環速度は1回転/月となります。（この設定はここでは不要なのですが、現実の経済を考えるときに必要となります）
• 水路から水があふれることはありません。水源からは水が無限に湧き出し、貯水池の容量は無限大です。
• 水源と貯水池以外に発散・吸収の要素は存在しません。

この流入量と流出量、および貯水池で計測された水量が与えられます。

• 水源から一定期間に流れ出た水量A。
• 収束水路を一定期間に流れる水量B。
• 貯水池の水量C。

選択肢（概算式）

概算式1、(A+B)/A

概算式2、(A+B)/C

両者の式では、分子がA+Bで共通しています。水源から水路に流入した水量がAで、貯水池と水源の間で計測された水量がBなので、広大な水路のどこかに適切な断面を設定すれば、A+Bの水量が計測されます。

問題は分母です。概算式1では、分母にAをとり、水路を流れている水量A+BがAの何倍であるかを計算しています。これは言い換えると、流入した水量Aがどの程度の期間（循環回数）、水路にとどまるのかを計算しています。概算式1は、水路を何回転すれば水路から貯水池に流れ出るかを計算しています。

流体で考えることが不慣れならば、例えば粒子的に、それもごく単純にAをボール1個、Bをボール2個とでも考えてください。

概算式2では、貯水池に貯まった水量Cを分母としています。Cは時間経過により増加するので、この概算式では、AとBが一定でも、時間が経過するほどに、得られる値は小さくなります。これでは、水源からの水量Aが水路を何回転しているかは計算できません。計算に不適切なこの概算式を出した理由は、経済学における貨幣の循環速度がこの計算方法を採用しているからです。

本問題の意味

今回のクイズは、経済学の貨幣の循環速度の導出方法を、流体的に置き換えたものです。今回のA+Bは、経済学のY=C+G+I=C+T+Sを置き換えたものです。もっといえば、A=G+I、B=Cと置き換えています。（今回採用したCと経済学のCが混ざってていすいません。）

これまでの記事で私が提案している計算方法は概算式1、経済学で採用している計算方法は概算式2です。完全に概算式2とイコールではないのですが、概算式１でないことは確かです。「私が採用している」と書きましたが、この概算は科学者技術者が普通に採用するであろう見積もりです。この記事で主張したいことは、以下の二点です。

1. こんなおかしな見積もりをする学問が経済学と呼ばれている。
2. 経済学を基盤とする経済政策によって、特に日本において国民生活は脅かされ続け、科学技術の発展は阻害されている。

この短い記事で、経済学のもろもろの拙さを詳細には書けません。概算式２として示した経済学の貨幣の循環速度の導出についても、科学者技術者の皆さんは「そんなおかしな見積もりをする定量的な学問が存在するわけないだろ、いい加減にしろ！（ドンッ）」と思われるかもしれません。しかし残念ながらこれは現実です。この貨幣循環についてのおかしな計算方法が100年も議論され続けていることを、科学者技術者のみなさんは信じられますか？

私が科学者技術者のみなさんにお勧めすることは、一か月、なんとか時間を作って学部生向けの経済学の教科書を読んでください。一年間、例えばなぜ「Y=C+G+I=C+T+S」で経済規模が測定できるのか、考えてください。「物質的に豊かになる」とは、定量的に何を意味するのか、どう測定するのか、考えてみてください。研究の出発点になりえる仮説の材料は多くありません。参考までに、既存の経済学の知識の範囲で私はこう考えました。

（経済学の教科書にはいろいろなトピックが挙げられていますが、それらが統一されたものの見方、一つの仮説によって統一的に記述されているわけではありません。私にはミクロ経済学の原理（需要と供給の均衡）でマクロ経済学の現象（貨幣循環）を説明しようとして、失敗し続けているように見えます。）

日本人の科学者技術者が１年間まじめに研究すれば、それで終了です。今の経済学よりもずっとましな科学的経済学の基盤はできました。お疲れさまでした。「失われた３０年間」は再来しません。科研費や企業研究費も増えて研究し放題、とはいきませんが再び日本は先進諸国として、科学技術をけん引することができるでしょう。

この期待される経済学の変化は、かつて科学がもたらした変化同様、不可逆的な認識の変化です。天動説から地動説への変化です。それと同じように、我々は、科学技術による不可逆的な認識の変化を経済と経済学にもたらすことができます。そして、我々の生活は「致命的に」良くなるでしょう。かつての科学による認識の変化同様、ある種の権力者達にとっては文字通り致命的です。

経済、つまり人類による商業活動も自然現象の範疇です。経済学で起きていることは、何一つ、宇宙の法則を乱してはいません（とりあえずそう仮定してみましょう）。それとも「経済は複雑だから科学的に研究することは難しい」なんて数学的証明を、みなさんどこかで見かけましたか？

およそ100年前に量子力学が形成されたように、現在が科学的経済学が形成される時期でもおかしくありません。データサイエンスやAIも面白いです。研究を楽しんでください！

【貨幣循環】の記事を読む順番

自然現象としての経済活動

本記事では、人類の経済活動が自然現象の範疇にあることを主張したい。

1. 人類が作り出した建築物について

人類の経済活動が自然現象の範疇にあることは、人類のすべての活動が自然法則を超越していないことに由来する。

ここでは建築物を例に挙げよう。建築物は、人類活動が無ければ自然界には存在せず、人類のあらゆる活動の象徴とみなすことができる。世界的には古代ピラミッドや、ローマの水道橋と闘技場を有名な例として、各国にはその国の歴史を代表する建築物が存在する。日本ならば古墳に寺社仏閣、城郭と城跡、そして現代では東京スカイツリーに始まり、高速道路、新幹線と在来線の線路網に加え、その他多くの建築物、何よりも民家！、が存在する。

しかし、どの建築物の機能も自然現象の範疇にあり、自然法則を超越したものは存在しない。私は現代の建築物についての詳細な知識など持たないが、主に使用されている材料はコンクリートや鉄骨（合金？）、木材、そしてガラスだろうか。現在の科学水準を逸脱した材料が日本の建築物に使われている、という話は聞いたことがない。そしてこれら建築物の機能や耐久年数もとうぜん材料に由来する。

我々の人類の最新の技術力は自然の法則を効率的に活用しているが、自然法則を超越してはいない。このことは当然なこと、極めて自然なことである。多くの読者、一般の皆さんは改めて議論するまでもないと思うかもしれない。

では、この認識を経済方向に拡張しよう。つまり、人類の経済活動も自然現象の範疇を超えてはいない、と認識しよう。

2. 人類の経済活動の複雑さ

日本の経済学者は、科学技術の発展および世界経済の発展と対照的な日本経済の低迷について質問されるとこう答えたことがあった

”経済は（自然現象よりも）複雑なので”

さきほどの「人類の経済活動が自然現象の範疇にある」ことを考えると、この複雑さは十分に分析可能な複雑さであると期待される。なぜなら、科学者たちはそれ以上の複雑な自然現象全体を理解すべく（手を付けられる所あるいは興味のある所から始めたのが実態ではあるが）、研究をつづけ、その全体像をある程度理解しているからである。

日本の、そして人類の経済活動がどれだけ複雑に見えても、それは地球全体の自然活動に内包されるものである。私の妄想でいえば、ひょっとしたら人体と同程度に複雑かもしれない。しかし経済活動が、地球近傍および地球上での異なるタイムスケール空間スケールの中での物質とエネルギーの循環と生命の進化よりも複雑かと言われたら多くの人々は否定するだろう。少なくとも私は否定する。

「地球近傍地球上での異なるタイムスケール空間スケールの中での物質とエネルギーの循環と生命の進化」などと格好をつけて書いたが、もう少し具体的には、太陽の影響受ける地球近傍の宇宙空間と地球大気の相互作用、地球大気内の天候気候、海中を含めた全地球表面における生命活動、そして地球内部（表層近く）のマントルの動きによってもたらされる大陸移動や突発的な火山の噴火など、ここに書ききれないほどの個々の自然現象及びその相互作用を意味している。ここに書ききれないのが当然で、科学の研究対象は非常に幅広い。翻って経済学、マクロ経済学の研究対象がこれより複雑だとは思えない。

従って、ここでの主張として、科学的研究活動は経済学を十分に理解できる。現在の経済と経済学の発展の弱さ遅さは、経済学者が科学的手法を用いていないからである。

3. 経済学の迷走、本質的問題

蛇足な気もするが、他の記事の宣伝ついでに書いておこう。

経済学100年の成果として、より正確には100年前の成果として、国家経済の規模を以下の式で観測している。

Y = C+G+I = C+S+T

いわゆるGDP、国民総生産とはこのYの値である。

私が理解している限り、経済学の問題は、この式の大本を説明する仮説がないこと、この式を定量的に導く仮説がないことである。（そして時間的空間的スケールや効果の強さを定量的に考慮せずに、経済効果をアピールするだけの経済学者）

私のうつろな記憶では、ガス圧や電気抵抗は、粒子（電子原子分子）の平均自由工程から求めることができた。ただ経済学には、そのような経験的規則を説明するための原子論に相当するものがまだないのである。100年たっても存在していない。

私の仮説を紹介しよう。以下の図である。

矢印は貨幣の流れを示している。太さは貨幣の量を意味する。

この図は、マクロ経済学の循環フロー図（企業、家計、生産要素市場（労働市場）と財サービス市場から構成される）に、政府と金融市場を加え、貨幣の流れを示した図である。詳細な説明は以前の記事に任せるとして、この図なら、Y = C+G+I = C+S+Tを、1年の間に断面で測定された貨幣の量として説明できる。

またこの図の示すところは、政府と金融市場から、企業、家計、生産要素市場と財サービス市場へ流れ込む貨幣量が増えれば、GDPが成長するということである。政府と金融市場からの貨幣流が増えなければ、GDPという測定された貨幣量は増えない。「流れるプール」の水量のように、水を多く供給すればその分増えるだけである。つまりGDPは、個人の努力や企業の生産性とは無関係である。一年間に測定された貨幣量であるGDPは、ミクロ経済学とは無関係である。政府と金融市場からの貨幣流がGDPに対して一次の効果なら、公的金利は二次以下の効果であろう（現実になんの効果も無かった）。

これは、決して斬新なアイデアではなく、「貨幣の流れはこうなっている」という観察の結果、あるいは紙幣発行について法律的制限からの推測である。

そしてこの仮説、「政府と金融市場からの貨幣量が増えれば、GDPが成長する」ことは、政府支出Gの成長率と名目GDPの成長率の関係をよく示している。これが私が現時点で示せるマクロ経済学の「仮説と検証」である。

経済学者と名乗る人々が現在なすべきことは、Y=C+G+I＝C+S+TがGDPを測定できる根拠となる仮説を構築し、その仮説の検証の一つとして政府支出Gの成長率と名目GDPの成長率の関係を用いることである。

そしてさらなる「仮説と検証」の発展として考えられる方向は、「政府支出Gの成長率と名目GDPの成長率の関係」が時間平均した成分なので、政府支出Gの成長率と名目GDPの成長率の時間変動について、時間平均した成分とそれ以外の振動成分の説明の両立である。

蛇足ついでに、この先機会もないので書いておこう。

私の調べたところ、歴史的な経緯を見る限り、経済学の学問的認識は退化している。100年以上前、第一次世界大戦へときな臭い時代、その頃には我々がミクロ経済学と呼んでいる、「需要と供給の平衡」を基盤とする経済学は存在した。しかし欧州各国の経済学者たちが、おそらくは現在とは比較にならないくらいの激論を交わしても、国家経済成長は困難だった。それは当然で、ミクロ経済学は市場内の貨幣の流れ（あるいは企業間の貨幣の奪い合い）を考えたもので、国家経済を成長させるために複数の市場全体の貨幣量を増やすことはout of scopeだからである。

マクロ経済学は、そのような歴史的流れの中で、労働市場全体、財サービス市場全体、消費者全体、企業全体の貨幣の流れを考えるためにできた学問である。そして、Y = C+G+I = C+S+Tで国家の経済規模を測定することとなった。しかし現在のマクロ経済学にはMicrofoundation(ミクロ経済学的基礎づけ)という考えが流行しており、つまり「ミクロ経済学に基づかなければ、正しくない」と考えることが正当化されているらしい。私が調べたところ、数学的証明や定量的な理論的根拠は見当たらなかった。

世界中の経済学者はこのような認識にあり、経済政策はこれまでの経験による手工業レベルの操作である。経済学の学問としての質は低い。過去100年間の科学技術の発展に対して、経済学は何を発展させたのか理解できない。経済学において、数字を客観的な指標とした「仮説と検証」サイクルが機能していないことは明らかである。ここに科学者が活躍する余地は十分にある。特に、大学で窮乏を訴えているだけの日本人研究者は経済学を研究すべきである。むろん彼らが大学職員として研究もせずに（研究できずに）研究者人生を終えることも結構であり、この先の30年間文科省に対して交渉活動を続けることも結構である。

【貨幣循環】の記事を読む順番

【貨幣循環】実質GDPの増加に対応する貨幣量の増加

この記事では、実質GDP（財・サービスの数量）の増加のためには、財・サービスを購入するための貨幣量の増加も必要である事を示す。数量方程式を変形すると以下の関係式が得られる。

dP/P + dQ/Q = dM/M

dP/P がインフレ率の増加を示し、dQ/Q が財・サービスの数量（実質GDP）の成長率を示し、それらに対応して dM/M が貨幣量の増加を示す。

例えば、貨幣量が変化せずとも供給の減少によってインフレが発生する場合、dM/M=0に対して、dQ/Qが財・サービス数量の減少率を示し、dP/Pがインフレの増加率を示す。

【貨幣循環】名目GDPの増減と経済格差の増減の分離 その２

前回の記事「【貨幣循環】名目GDPの増減と経済格差の増減の分離　その１」では、名目GDPの増減と経済格差の増減が独立である事を、数式と観測値によって示しました。この記事では、独立な名目GDPと経済格差の増加と維持の組み合わせがどういう状況を引き起こすのかを議論します。以下の表がその状況のまとめです。

本記事では、政府支出及び名目GDPの減少は議論しません。どう考えても良い状況ではないので。

これらの組み合わせを導くために、人口と財・サービスの増減を経済格差の増減に結びつけて議論します。数式は出て来ないので、論理的に堅固ではありません。ただし、個人の能力の物理的な限界を用います。経済格差の増減と財・サービスの増減についての論理構成は次のようになります。

1. 人間の能力と行為には様々な物理的な限界が存在する。
2. 個人の認識能力と消費能力にも明確な限界が存在する。従って、少数の顧客（富裕層）よりも、桁違いに多数の顧客（中間層）の消費行動によって財・サービス市場に多くの貨幣が流れ込む。
3. 経済格差が小さく、中間層の経済的豊かさが継続するなら、貨幣循環によって消費に多くの貨幣流が流れ、衣食住に加えた豊富な財・サービスが更新・拡張される。

ここで中間層の有無は、平均消費性向βの分布の山型とL字型によって示されます。この経済格差と財・サービスについての議論と、前回の数式によって示した政府支出の増減に伴う名目GDPの増減の組み合わせをまとめたのが冒頭の表です。

【貨幣循環】貨幣循環速度Vの成長率

この記事の主題は、貨幣の循環速度Vと政府支出Gの平均成長率の関係である。以下の図は、33カ国20年間の平均値の分布。政府支出の平均成長率の範囲が2％から10%、そして循環速度Vの平均成長率の範囲はほぼ1%以下（2%超が一例）である。過去20年間において、「循環速度Vの成長率は、政府支出Gの成長率より小さい」という結果が得られた。

各国の政府支出の成長率の平均値（横軸）と貨幣循環速度の成長率の平均値（縦軸）。

データはOECDから取得した33カ国、20年間の平均値。ここでは世界規模の経済的な事件となった2009年と2020年を除外している。

このグラフで記事を書く理由は、「【貨幣循環】政府支出Gの成長率と名目GDPの成長率の関係（Y、M、Vの各変化率の関係）」において紹介した、政府支出と名目GDPの成長率の正比例関係を説明するためである。先の記事ではこの正比例関係の説明として、貨幣循環のもとでの循環速度の成長率が0で、政府支出と国内投資の成長率が同程度ならこの正比例関係を説明できる事を示した。今回のグラフは、循環速度の成長率が0とはいかないまでも、循環速度の成長率が政府支出の成長率に対して小さい事を示している。

内容

1. データ

2. 数式まとめ

3. グラフ

【貨幣循環】財・サービスの数量の概算

現在我々が1年間に消費している財・サービスの数量は、平均物価を100円から1000円と仮定して、およそ4000から40000程度である。1年を365日、さらに400日と大雑把にすれば、1日に消費あるいは購入している財・サービスの数量は10から100程度となる。この数字の導出を説明する。

内容。

1. 数量計算の意義
2. 拡張された数量方程式
3. 財・サービスの数量の試算

【貨幣循環】直接給付金による C+G+I と PQ の不一致

この記事の結論として、貨幣循環の流体的描像のもとでは、直接給付金によって「PQ < C+G+I」が導かれる。国内総生産としては、G から直接給付金の予算を引いた値を G' として、Y=C+G'+I=PQ を採用すべきだろう。

貨幣循環の流体的描像。Aに財・サービス市場が位置し、Bに家計が位置する。CとDは政府と金融市場である。

【貨幣循環】名目GDPの増減と経済格差の増減の分離 その１

この記事の結論は、「名目GDP（政府支出）の増減と経済格差の増減は切り分けましょう」、です。経済成長の議論ではしばしば「パイの大きさ」と「パイの切り方」の例えが使われますが、それは数式上で明確に分離できます。M=G+Iがパイの大きさであり、平均消費性向βの分布（所得分布）がパイの切り方です。

政府支出を増やして名目GDPが増加すれば自動的に経済格差が縮小するわけではなく、経済格差が縮小すれば名目GDPが必ず増加する訳ではありません。貨幣循環の描像からは、名目GDPの増減は貨幣流の総量の問題であり、経済格差の増減は貨幣流の配分の問題です。

この記事で扱う「名目GDPの増減と経済格差の増減の分離」を明確にすると、以下の表のように、国の発展（人口と財・サービスの増加）のために、政府支出と平均消費性向βの分布および所得分布がどのように作用するかを議論する事ができます。

この表については、次の記事で議論します。

「名目GDPの増減と経済格差の増減の分離」の根拠は、次の2つの方程式です。

• M=G+I
• V=Y/(G+I)=1/(1-β)

この数式の導出については、「【貨幣循環】貨幣循環導入の3点セット」を御覧ください。数量方程式のMをM=G+Iとおくと、貨幣循環のもとで循環フロー図とGDPの定義を関係づけられます。

内容

1. 動機
2. βの平均値とβの分布

【貨幣循環】名目GDPと M=G+I と V=1/(1-β) の成長率

「【貨幣循環】貨幣循環導入の3点セット」では、貨幣循環の定式化である M=G+I と V=1/(1-β) を紹介した。「【貨幣循環】歳出伸び率とGDP成長率の関係」では、名目GDPの成長率と政府支出Gの成長率の関係を紹介した。本記事では、MとV、および名目GDPの成長率について時間変化と散布図のグラフを紹介する。

名目GDPの成長率（縦軸）とM=G+Iの成長率（横軸）についての散布図。

これが名目GDPの成長率（縦軸）とM=G+Iの成長率（横軸）についての散布図である。M=G+Iと名目GDPの成長率が20%以下の範囲でよく正比例している事が分かる（一定の分散あり）。これは貨幣循環の因果関係として当然である。貨幣循環を考えれば、企業と家計による貨幣循環への貨幣の注入量そして吸収量がG+I＝S+Tだからである。

ただし、M=G+Iと名目GDPの成長率の1対1関係には、「Vの成長率（変化率）が低ければ」という注意書きがつく。M=G+Iが20%以上の範囲において、データ点が傾き1を示す破線から離れているのは、日本の1960年代以前のVの成長率が大きかったからである。そして上記の「一定の分散」というのはVの成長率の変動である。

この事から見出される結論の一つとして、近年の日本のGDPの低迷はM=G+I の低成長率に由来する。

内容。

1. M=G+I と V=1/(1-β) の変化率
2. 日本とアメリカの名目GDPの成長率
3. V の成長率の特徴

【貨幣循環】マクロ経済学とミクロ経済学の構図まとめ

最近の記事中で、マクロ経済学とミクロ経済学の関係についての言及が増えたので、ここにまとめる。

1. マクロ経済学とは貨幣循環である。Y=C+G+Iと循環フロー図とY=MVより、M=G+I、V=1/(1-β)。（【貨幣循環】貨幣循環導入の3点セット）

【貨幣循環】貨幣と労働力と資源の循環、および需要と供給の定量化

マクロ経済学の冒頭では循環フロー図が紹介され、企業と家計と市場の関係が貨幣循環として認識される。本記事では、貨幣の循環と同様に経済学に欠かせない概念を紹介する。それは労働力と資源の循環である。そしてこの三種類の循環のもとで、財・サービス市場における需要と均衡について提案を行う。

1. 貨幣と労働力と資源の循環

以下の三つの図は、貨幣と労働力と資源の循環を示している。

貨幣の循環。

【貨幣循環】拡張された数量方程式、フィリップス曲線、マクロ経済学とミクロ経済学の接続

この記事の主張は二点。一点はフィリップス曲線について、もう一点はマクロ経済学（貨幣循環）とミクロ経済学の接続について、である。

拡張された数量方程式からは、収入のインフレ率（年変化率）と就業者数の年変化率がペアの変数として得られる。理論的根拠のない、物価のインフレ率と失業率の関係を議論するよりも、数量方程式によって導かれた収入の年変化率と就業者数の年変化率の配分を研究すべきである。

この収入の年変化率と就業者数の年変化率の配分のメカニズムについては、少なくとも今の筆者の理解では、貨幣循環で描像できない。これはミクロ経済学の領域である。拡張された数量方程式（MV = PQ = NO = PSN'）は、マクロ経済学とミクロ経済学の接続を示している。

【貨幣循環】貨幣循環と循環速度の実態

 「【貨幣循環】貨幣循環導入の3点セット」において、日本の2017年の貨幣の循環速度 V=Y/(G+I)～2.2、という値を得た。この記事では、この値の実態について議論したい。これはつまりV~2.2の単位についての議論である。読者に主張したい事は、次の2点である。

1. 循環フロー図で表される貨幣循環の実態は、数字の移動である。
2. 貨幣の循環速度の実態は、商習慣の月収制に強くコントロールされている。

【電子書籍】マクロフロー経済学 A1 科学者と技術者が経済学を学びそして駆逐すべき理由

マクロフロー経済学　A1　科学者と技術者が経済学を学びそして駆逐すべき理由

Macro-Flow Economics A1 Why Science and Technology should reject Economics

GooglePlay, GoogleeBooks、販売価格：無料

【貨幣循環】政府債務残高と名目GDPとの比率を数式で解く

こちらのグラフは、財務省が公開している政府債務残高の名目GDP比です（こちらのページ）。財務省はこの政府債務残高を「借金」と称して、「日本の比率は世界でも高い値であり、借金が膨張すると日本の財政が破綻する」と述べています。そして、財政破綻を避けるために財務省は政府支出を抑制しよう、債務残高の膨張を抑制しようとしています。

今回の数式展開からの理解できる事として、現在の諸数値のもと、政府支出Gを増やして名目GDPを増加させると、この比は減少します。そして、政府支出を減少させれば名目GDPも減少し、この比は増加します。この原因は、政府債務残高がすでに膨大な値だからです。政府支出の変動に対して政府債務残高の変動幅は小さく、一方で名目GDPの変化幅が大きいからです。

経済成長における成長率「GDP ＞ 平均所得 ＞ 物価」の理論的背景

日本の経済統計と転換点
「先進国型「経済成長の条件」とは」

GDP・家計消費 ＞ 労働生産性・平均所得 ＞物価

当然ですが、この関係で経済成長するのが普通ですね。
どの先進国も低成長ですが、この関係です。

経済停滞中の日本だけ、平均所得が最も減っています。https://t.co/MLf3k6Od9T

— 小川製作所 (@OgawaSeisakusho) January 17, 2022

本記事の動機は、小川製作所さん (@OgawaSeisakusho) による経済成長の成長率のグラフです。それらのグラフでは、

• GDP ＞ 平均所得 ＞ 物価

という変化率が一般的のようです。この関係を拡張された数量方程式を使って説明します。家計消費については第3節で説明します。労働生産性は単位時間の変数なので、ここでは議論しません。内容は次の通りです。

1. 拡張された数量方程式による説明
2. 変化率の関係式の導出
3. GDPと家計消費の関係

【貨幣循環】流体的貨幣循環と直接給付とインフレターゲット

以下の図は、貨幣循環を流体感覚で描像する事を目的とします。個人的な目的は、直接給付金の作用を理解するためです。一方でこの試みは、流体力学や電子回路に馴染んでいる科学者と技術者の貨幣循環についての理解を助ける事ができるでしょう。筆者としても、時間変化についてはこちらの描像のほうが理解しやすいように思います。

1. 流体的貨幣循環

貨幣流は非圧縮性流体と考えます。

流体的貨幣循環

【貨幣循環】貨幣循環導入の3点セット

本記事では、貨幣循環導入の3点セット、循環フロー図、名目GDPの定義、数量方程式、について説明し、日本経済の貨幣循環の概要を定量的に示す。この3点セットは現代経済学において独立した項目として扱われているが、これらを貨幣循環の観点から統合する。結論として、M = G+I = S+T である。

本記事の内容は以下の通りである。

1. 3点セットの説明。
2. 3点セットによる貨幣循環の描像。
3. 二種類の貨幣流。
4. 名目GDPから分かる貨幣循環の概要。

【貨幣循環】政府支出Gの成長率と名目GDPの成長率の関係（Y、M、Vの各変化率の関係）

内容。

1. ある関係。
2. 貨幣循環による説明。
3. dV/V=0 and M=aG

1. ある関係

今回の記事の動機は、以下の図。

非常に面白いのは、歳出（国家予算、G）の成長率と名目GDP（Y）の成長率が1対1である事。この図にプロットされているデータは、31カ国の20年間平均のデータである。本記事では、この関係について貨幣循環の観点で説明する。