【貨幣循環】名目GDPの増減と経済格差の増減の分離 その２

前回の記事「【貨幣循環】名目GDPの増減と経済格差の増減の分離　その１」では、名目GDPの増減と経済格差の増減が独立である事を、数式と観測値によって示しました。この記事では、独立な名目GDPと経済格差の増加と維持の組み合わせがどういう状況を引き起こすのかを議論します。以下の表がその状況のまとめです。

本記事では、政府支出及び名目GDPの減少は議論しません。どう考えても良い状況ではないので。

これらの組み合わせを導くために、人口と財・サービスの増減を経済格差の増減に結びつけて議論します。数式は出て来ないので、論理的に堅固ではありません。ただし、個人の能力の物理的な限界を用います。経済格差の増減と財・サービスの増減についての論理構成は次のようになります。

1. 人間の能力と行為には様々な物理的な限界が存在する。
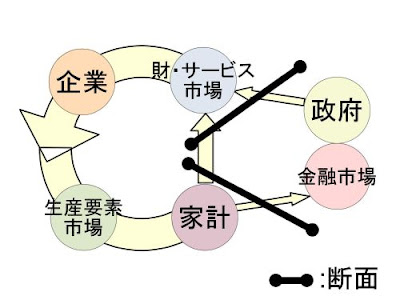
2. 個人の認識能力と消費能力にも明確な限界が存在する。従って、少数の顧客（富裕層）よりも、桁違いに多数の顧客（中間層）の消費行動によって財・サービス市場に多くの貨幣が流れ込む。
3. 経済格差が小さく、中間層の経済的豊かさが継続するなら、貨幣循環によって消費に多くの貨幣流が流れ、衣食住に加えた豊富な財・サービスが更新・拡張される。

ここで中間層の有無は、平均消費性向βの分布の山型とL字型によって示されます。この経済格差と財・サービスについての議論と、前回の数式によって示した政府支出の増減に伴う名目GDPの増減の組み合わせをまとめたのが冒頭の表です。

【貨幣循環】貨幣循環速度Vの成長率

この記事の主題は、貨幣の循環速度Vと政府支出Gの平均成長率の関係である。以下の図は、33カ国20年間の平均値の分布。政府支出の平均成長率の範囲が2％から10%、そして循環速度Vの平均成長率の範囲はほぼ1%以下（2%超が一例）である。過去20年間において、「循環速度Vの成長率は、政府支出Gの成長率より小さい」という結果が得られた。

各国の政府支出の成長率の平均値（横軸）と貨幣循環速度の成長率の平均値（縦軸）。

データはOECDから取得した33カ国、20年間の平均値。ここでは世界規模の経済的な事件となった2009年と2020年を除外している。

このグラフで記事を書く理由は、「【貨幣循環】政府支出Gの成長率と名目GDPの成長率の関係（Y、M、Vの各変化率の関係）」において紹介した、政府支出と名目GDPの成長率の正比例関係を説明するためである。先の記事ではこの正比例関係の説明として、貨幣循環のもとでの循環速度の成長率が0で、政府支出と国内投資の成長率が同程度ならこの正比例関係を説明できる事を示した。今回のグラフは、循環速度の成長率が0とはいかないまでも、循環速度の成長率が政府支出の成長率に対して小さい事を示している。

内容

1. データ

2. 数式まとめ

3. グラフ

【貨幣循環】財・サービスの数量の概算

現在我々が1年間に消費している財・サービスの数量は、平均物価を100円から1000円と仮定して、およそ4000から40000程度である。1年を365日、さらに400日と大雑把にすれば、1日に消費あるいは購入している財・サービスの数量は10から100程度となる。この数字の導出を説明する。

内容。

1. 数量計算の意義
2. 拡張された数量方程式
3. 財・サービスの数量の試算

【貨幣循環】直接給付金による C+G+I と PQ の不一致

この記事の結論として、貨幣循環の流体的描像のもとでは、直接給付金によって「PQ < C+G+I」が導かれる。国内総生産としては、G から直接給付金の予算を引いた値を G' として、Y=C+G'+I=PQ を採用すべきだろう。

貨幣循環の流体的描像。Aに財・サービス市場が位置し、Bに家計が位置する。CとDは政府と金融市場である。

【貨幣循環】名目GDPの増減と経済格差の増減の分離 その１

この記事の結論は、「名目GDP（政府支出）の増減と経済格差の増減は切り分けましょう」、です。経済成長の議論ではしばしば「パイの大きさ」と「パイの切り方」の例えが使われますが、それは数式上で明確に分離できます。M=G+Iがパイの大きさであり、平均消費性向βの分布（所得分布）がパイの切り方です。

政府支出を増やして名目GDPが増加すれば自動的に経済格差が縮小するわけではなく、経済格差が縮小すれば名目GDPが必ず増加する訳ではありません。貨幣循環の描像からは、名目GDPの増減は貨幣流の総量の問題であり、経済格差の増減は貨幣流の配分の問題です。

この記事で扱う「名目GDPの増減と経済格差の増減の分離」を明確にすると、以下の表のように、国の発展（人口と財・サービスの増加）のために、政府支出と平均消費性向βの分布および所得分布がどのように作用するかを議論する事ができます。

この表については、次の記事で議論します。

「名目GDPの増減と経済格差の増減の分離」の根拠は、次の2つの方程式です。

• M=G+I
• V=Y/(G+I)=1/(1-β)

この数式の導出については、「【貨幣循環】貨幣循環導入の3点セット」を御覧ください。数量方程式のMをM=G+Iとおくと、貨幣循環のもとで循環フロー図とGDPの定義を関係づけられます。

内容

1. 動機
2. βの平均値とβの分布

【貨幣循環】名目GDPと M=G+I と V=1/(1-β) の成長率

「【貨幣循環】貨幣循環導入の3点セット」では、貨幣循環の定式化である M=G+I と V=1/(1-β) を紹介した。「【貨幣循環】歳出伸び率とGDP成長率の関係」では、名目GDPの成長率と政府支出Gの成長率の関係を紹介した。本記事では、MとV、および名目GDPの成長率について時間変化と散布図のグラフを紹介する。

名目GDPの成長率（縦軸）とM=G+Iの成長率（横軸）についての散布図。

これが名目GDPの成長率（縦軸）とM=G+Iの成長率（横軸）についての散布図である。M=G+Iと名目GDPの成長率が20%以下の範囲でよく正比例している事が分かる（一定の分散あり）。これは貨幣循環の因果関係として当然である。貨幣循環を考えれば、企業と家計による貨幣循環への貨幣の注入量そして吸収量がG+I＝S+Tだからである。

ただし、M=G+Iと名目GDPの成長率の1対1関係には、「Vの成長率（変化率）が低ければ」という注意書きがつく。M=G+Iが20%以上の範囲において、データ点が傾き1を示す破線から離れているのは、日本の1960年代以前のVの成長率が大きかったからである。そして上記の「一定の分散」というのはVの成長率の変動である。

この事から見出される結論の一つとして、近年の日本のGDPの低迷はM=G+I の低成長率に由来する。

内容。

1. M=G+I と V=1/(1-β) の変化率
2. 日本とアメリカの名目GDPの成長率
3. V の成長率の特徴

【貨幣循環】マクロ経済学とミクロ経済学の構図まとめ

最近の記事中で、マクロ経済学とミクロ経済学の関係についての言及が増えたので、ここにまとめる。

1. マクロ経済学とは貨幣循環である。Y=C+G+Iと循環フロー図とY=MVより、M=G+I、V=1/(1-β)。（【貨幣循環】貨幣循環導入の3点セット）

【貨幣循環】貨幣と労働力と資源の循環、および需要と供給の定量化

マクロ経済学の冒頭では循環フロー図が紹介され、企業と家計と市場の関係が貨幣循環として認識される。本記事では、貨幣の循環と同様に経済学に欠かせない概念を紹介する。それは労働力と資源の循環である。そしてこの三種類の循環のもとで、財・サービス市場における需要と均衡について提案を行う。

1. 貨幣と労働力と資源の循環

以下の三つの図は、貨幣と労働力と資源の循環を示している。

貨幣の循環。

【貨幣循環】拡張された数量方程式、フィリップス曲線、マクロ経済学とミクロ経済学の接続

この記事の主張は二点。一点はフィリップス曲線について、もう一点はマクロ経済学（貨幣循環）とミクロ経済学の接続について、である。

拡張された数量方程式からは、収入のインフレ率（年変化率）と就業者数の年変化率がペアの変数として得られる。理論的根拠のない、物価のインフレ率と失業率の関係を議論するよりも、数量方程式によって導かれた収入の年変化率と就業者数の年変化率の配分を研究すべきである。

この収入の年変化率と就業者数の年変化率の配分のメカニズムについては、少なくとも今の筆者の理解では、貨幣循環で描像できない。これはミクロ経済学の領域である。拡張された数量方程式（MV = PQ = NO = PSN'）は、マクロ経済学とミクロ経済学の接続を示している。

【貨幣循環】貨幣循環と循環速度の実態

 「【貨幣循環】貨幣循環導入の3点セット」において、日本の2017年の貨幣の循環速度 V=Y/(G+I)～2.2、という値を得た。この記事では、この値の実態について議論したい。これはつまりV~2.2の単位についての議論である。読者に主張したい事は、次の2点である。

1. 循環フロー図で表される貨幣循環の実態は、数字の移動である。
2. 貨幣の循環速度の実態は、商習慣の月収制に強くコントロールされている。

【電子書籍】マクロフロー経済学 A1 科学者と技術者が経済学を学びそして駆逐すべき理由

マクロフロー経済学　A1　科学者と技術者が経済学を学びそして駆逐すべき理由

Macro-Flow Economics A1 Why Science and Technology should reject Economics

GooglePlay, GoogleeBooks、販売価格：無料

【貨幣循環】政府債務残高と名目GDPとの比率を数式で解く

こちらのグラフは、財務省が公開している政府債務残高の名目GDP比です（こちらのページ）。財務省はこの政府債務残高を「借金」と称して、「日本の比率は世界でも高い値であり、借金が膨張すると日本の財政が破綻する」と述べています。そして、財政破綻を避けるために財務省は政府支出を抑制しよう、債務残高の膨張を抑制しようとしています。

今回の数式展開からの理解できる事として、現在の諸数値のもと、政府支出Gを増やして名目GDPを増加させると、この比は減少します。そして、政府支出を減少させれば名目GDPも減少し、この比は増加します。この原因は、政府債務残高がすでに膨大な値だからです。政府支出の変動に対して政府債務残高の変動幅は小さく、一方で名目GDPの変化幅が大きいからです。

低体温症になりかけた話

今朝、室内で低体温症になりかけました。備忘録として残しておきます。

症状としては、動悸、横になっていられず無闇に動き回る、錯乱一歩手前、でした。私は錯乱した事はありませんが、本当に叫び出したい、気を抜くと今の自分を失うという予感を強く感じました。後は、体の中がむず痒く？、気持ち悪く、血管を切って血を抜きたい衝動も感じました。動き回る事に加え、外に走りに出かけたいとも感じたのですが、無意識に体温をあげようとしていたようです。

感じなかった事は手足と身体の冷えです。しばらくして救急車を呼ぶ準備として体温を測ったところ、36.0度でした。そこでコタツに入り込んだところ、身体が楽になりました。その後湯たんぽを作り布団に入り、気づくと、湯たんぽをお腹に乗せた状態で目が覚めました。幸いに全ての症状は消えていました。

その後検索で調べ、低体温症の一歩二歩手前だったと判断しました。

低体温症 - 25. 外傷と中毒 - MSDマニュアル家庭版

原因は、冷え切った部屋で、布団に隙間がある状態で寝ていた事です。前日に筋トレを実施して疲れ切っていた事がきっかけかもしれません。今夜からは湯たんぽで寝ます。

経済成長における成長率「GDP ＞ 平均所得 ＞ 物価」の理論的背景

日本の経済統計と転換点
「先進国型「経済成長の条件」とは」

GDP・家計消費 ＞ 労働生産性・平均所得 ＞物価

当然ですが、この関係で経済成長するのが普通ですね。
どの先進国も低成長ですが、この関係です。

経済停滞中の日本だけ、平均所得が最も減っています。https://t.co/MLf3k6Od9T

— 小川製作所 (@OgawaSeisakusho) January 17, 2022

本記事の動機は、小川製作所さん (@OgawaSeisakusho) による経済成長の成長率のグラフです。それらのグラフでは、

• GDP ＞ 平均所得 ＞ 物価

という変化率が一般的のようです。この関係を拡張された数量方程式を使って説明します。家計消費については第3節で説明します。労働生産性は単位時間の変数なので、ここでは議論しません。内容は次の通りです。

1. 拡張された数量方程式による説明
2. 変化率の関係式の導出
3. GDPと家計消費の関係

【貨幣循環】流体的貨幣循環と直接給付とインフレターゲット

以下の図は、貨幣循環を流体感覚で描像する事を目的とします。個人的な目的は、直接給付金の作用を理解するためです。一方でこの試みは、流体力学や電子回路に馴染んでいる科学者と技術者の貨幣循環についての理解を助ける事ができるでしょう。筆者としても、時間変化についてはこちらの描像のほうが理解しやすいように思います。

1. 流体的貨幣循環

貨幣流は非圧縮性流体と考えます。

流体的貨幣循環

【貨幣循環】貨幣循環導入の3点セット

本記事では、貨幣循環導入の3点セット、循環フロー図、名目GDPの定義、数量方程式、について説明し、日本経済の貨幣循環の概要を定量的に示す。この3点セットは現代経済学において独立した項目として扱われているが、これらを貨幣循環の観点から統合する。結論として、M = G+I = S+T である。

本記事の内容は以下の通りである。

1. 3点セットの説明。
2. 3点セットによる貨幣循環の描像。
3. 二種類の貨幣流。
4. 名目GDPから分かる貨幣循環の概要。

【貨幣循環】政府支出Gの成長率と名目GDPの成長率の関係（Y、M、Vの各変化率の関係）

内容。

1. ある関係。
2. 貨幣循環による説明。
3. dV/V=0 and M=aG

1. ある関係

今回の記事の動機は、以下の図。

非常に面白いのは、歳出（国家予算、G）の成長率と名目GDP（Y）の成長率が1対1である事。この図にプロットされているデータは、31カ国の20年間平均のデータである。本記事では、この関係について貨幣循環の観点で説明する。

【貨幣循環】名目GDPの定義の統合と拡張された数量方程式

本記事の内容は、「マクロフロー経済学　３　貨幣循環の定量解析」の第3章の一部を含む。

本記事では、前記事「GDPと国家予算は膨張する」での理論的根拠とした拡張された数量方程式の導出について説明する。その出発点は、循環フロー図中におけるGDPの定義の統合である。本記事の内容は以下の通りである。

1. 循環フロー図とGDPの定義の統合
2. 拡張された数量方程式